Why DiscoCal?

For decades, the checkerboard pattern has been regarded as the standard method for camera calibration, offering only pixel-level precision. But what if we could push the limits of accuracy even further?
DiscoCal reveals the power of the circular pattern — a game-changer that enables subpixel precision, even for challenging sensors such as thermal or cameras with high-distortions.

Advantages of the Circular Pattern

The checkerboard pattern uses the corners of squares as control points.
However, these corners are only accurate to the pixel level, as shown below:

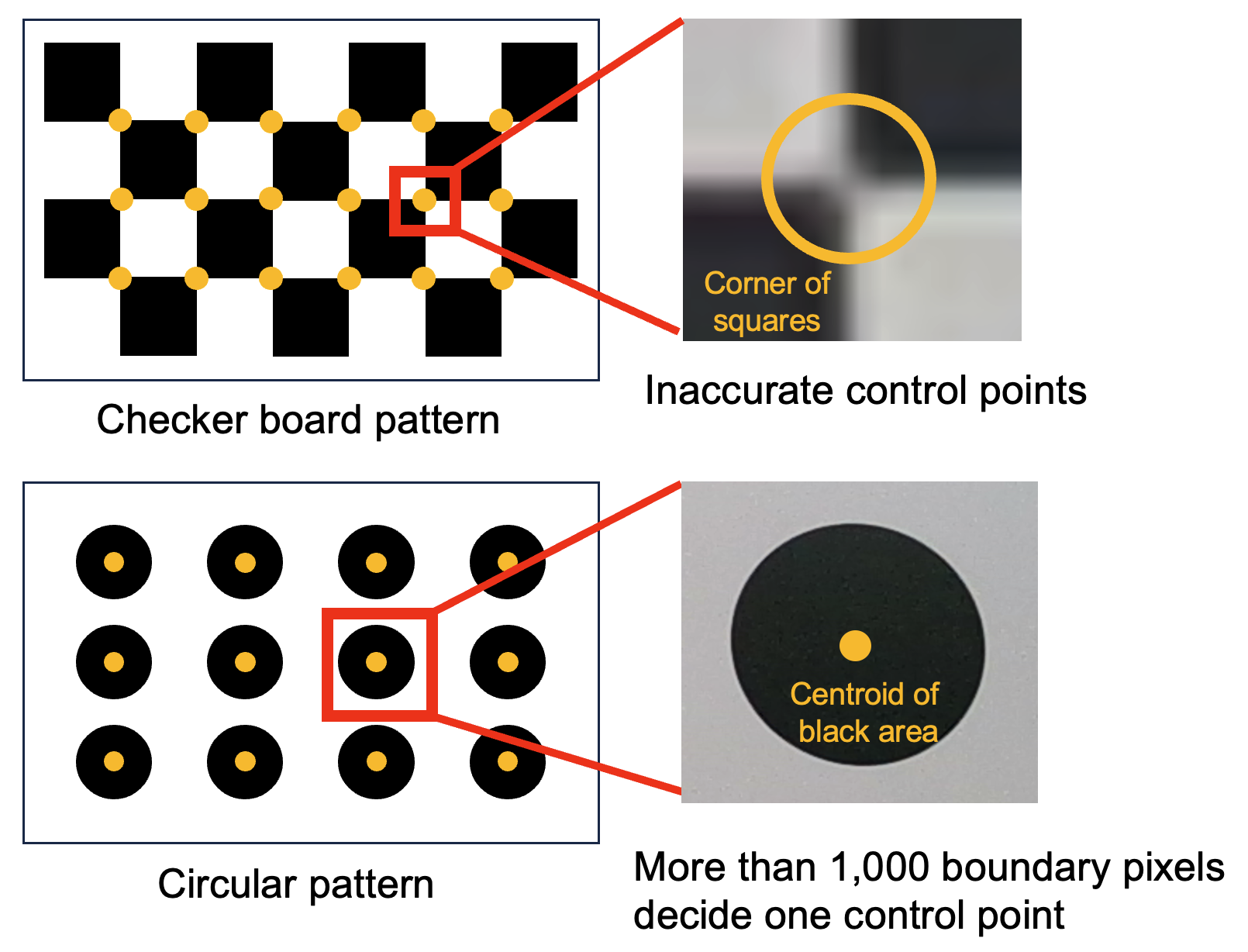
In contrast, the circular pattern uses the centroids of circular shapes, which can be detected with subpixel accuracy.

Unbiased Projection Model

Subpixel accuracy and detection robustness are key strengths of conics features.
So why has the checkerboard remained dominant over the circular pattern?

😢 Conics are no longer true conics under lens distortion!

As shown below, due to perspective and lens distortion, the projected center of a circle no longer coincides with the centroid of the resulting ellipse.

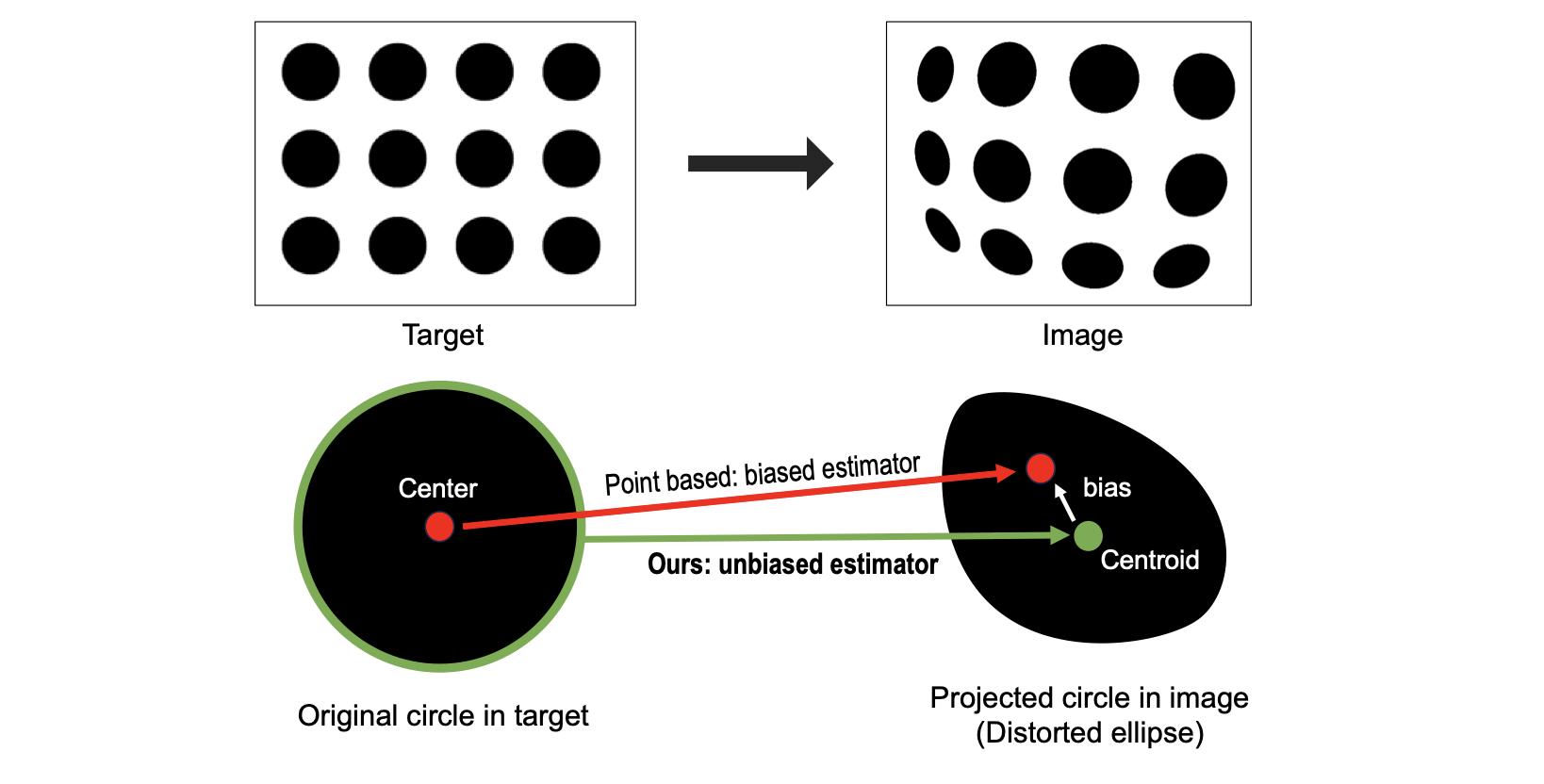
Most calibration methods using circualr patterns ignore the geometry of the distorted ellipse, leading to bias and lower calibration accuracy than checkerboard methods.

📌 Our unbiased estimator fills the missing piece in conic-based calibration.

This paper introduces an unbiased projection model for circular patterns using a probabilistic concept called moments.
Although there is no simple analytic form for distorted ellipses, moment representations always exist.

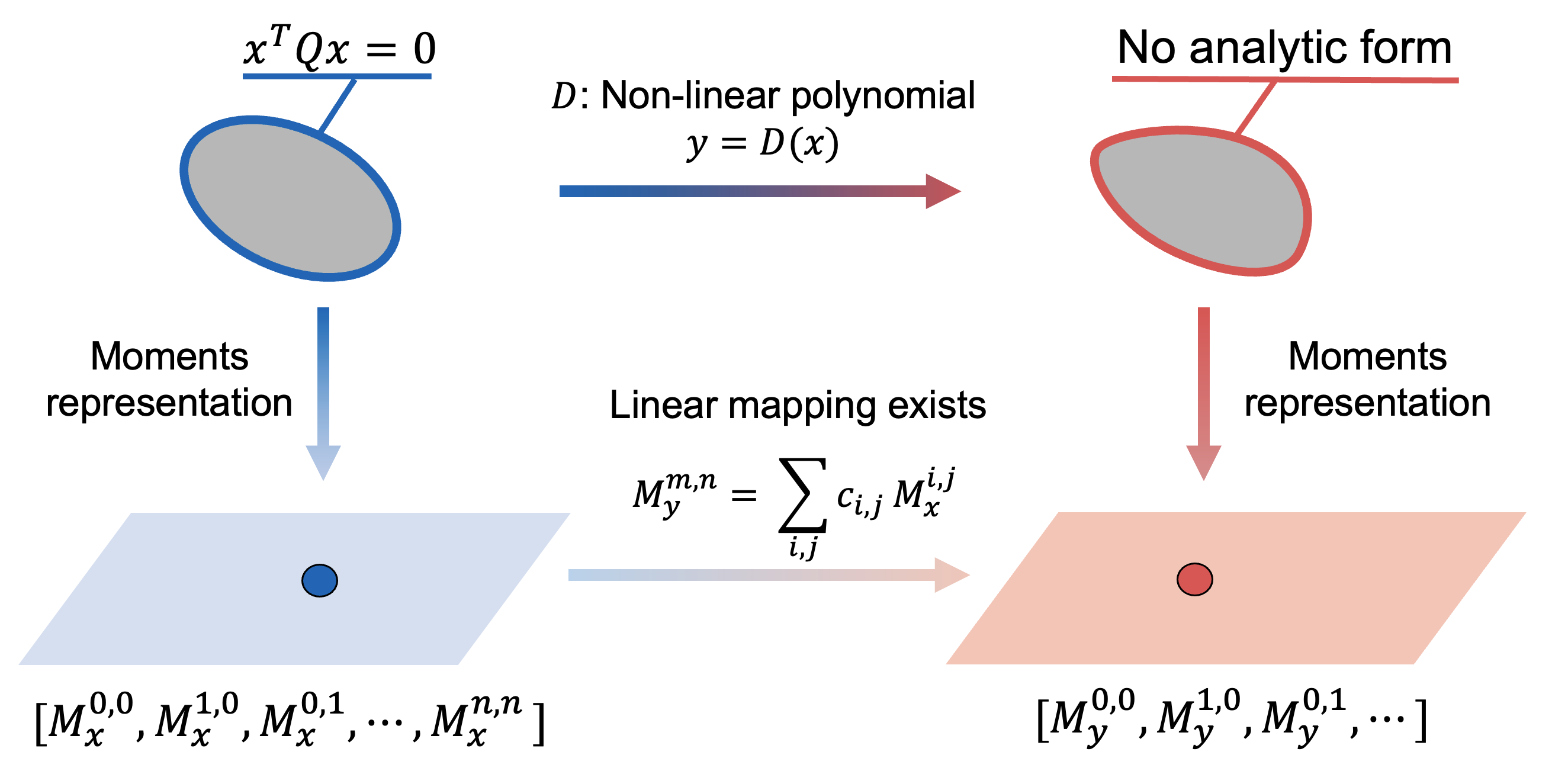
If you are interested in the unbiased projection of conic, please visit our paper

Uncertainty-aware Framework

Even when using a circular pattern, it is impossible to obtain ideal measurements from real-world images.
Therefore, incorporating measurement uncertainty into the calibration process enhances both overall accuracy and robustness.

DiscoCal is the first method to define and utilize the uncertainty of circular pattern detection.
It provides not only the calibration parameters, but also the standard deviation (i.e., uncertainty) for each parameter, as shown below (when \(n_d=2\)) :

Parameter	fx	fy	cx	cy	skew	d1	d2	d3	d4
Mean	491.2	491.4	725.9	570.0	0.60	-0.008	0.002	0	0
\(2\sigma\)	0.94	0.91	0.30	0.38	0.104	0.0009	0.0006	0	0

You can also check the calibration uncertainty in image space.
After calibration, DiscoCal generates an uncertainty map, which indicates the pixel-wise accuracy of the calibration.

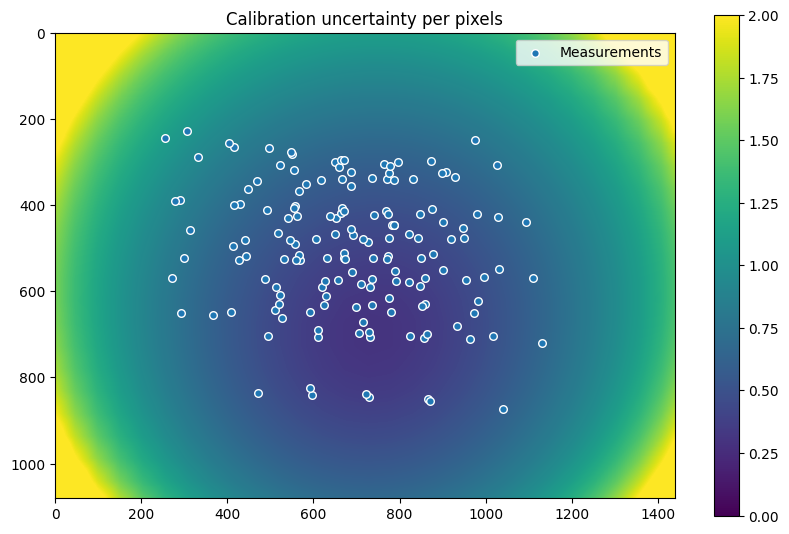
If you are interested in the uncertainty in calibration, please visit our paper